Long Division Steps Printable

Hey there, today I want to talk about a fundamental concept in math - long division. It can seem daunting at first, but with a bit of practice, it becomes easier and can even be enjoyable!

Long Division Basics

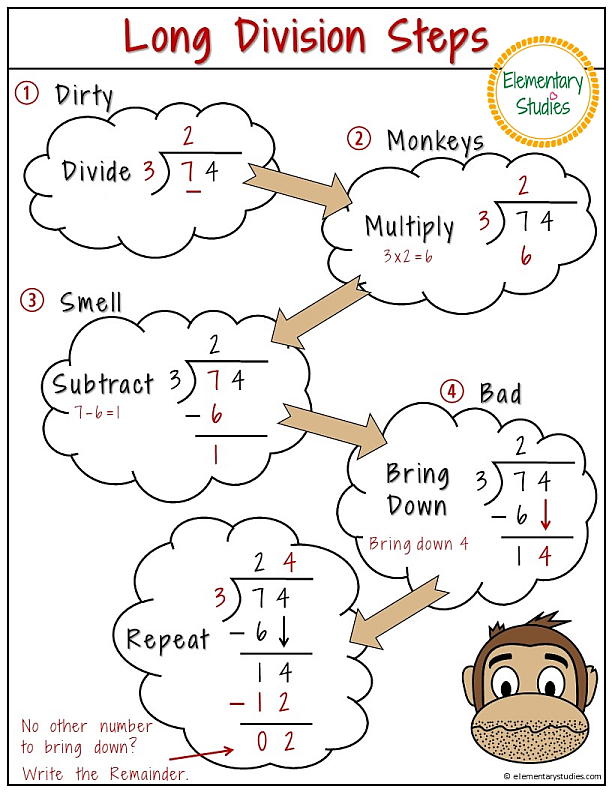Before diving into the steps of long division, let’s review the basic terminology involved.

• Dividend: The number being divided.
• Divisor: The number dividing the dividend.
• Quotient: The answer to the division problem.
• Remainder: The amount left over after division is completed.

The Steps of Long Division

Now that we know the terms, let’s walk through the steps of long division.

1. Write the dividend inside the long division symbol, and the divisor outside of it.
2. Divide the leftmost digit of the dividend by the divisor, and write the resulting quotient above the digit. If the divisor doesn’t evenly divide into the leftmost digit, add a zero as a placeholder above the digit and continue to the next digit.
3. Multiply the divisor by the quotient digit, and write the result under the leftmost digit of the dividend.
4. Subtract the result of step 3 from the leftmost digits of the dividend.
5. Bring down the next digit of the dividend next to the result from step 4.
6. Repeat steps 2-5 until there are no digits left in the dividend or the remainder is less than the divisor.
7. If there are no digits left in the dividend, the quotient and remainder are the final answer. If there is a remainder less than the divisor, it becomes the final remainder.

Example

Let’s run through an example using the numbers 345 and 6.

So our final answer is 57 with a remainder of 3.

Practice

Now that we understand the steps, it’s time to practice! Here are some long division problems to try:

• 786 / 3
• 1584 / 8
• 5823 / 17

Once you’ve given them a shot, check your answers below.

• 786 / 3 = 262 with no remainder
• 1584 / 8 = 198 with no remainder
• 5823 / 17 = 342 with a remainder of 9

Remainders

What do we do with remainders? It depends on the context of the problem. In some cases, we may round up or down, but in other cases, we may need to leave the remainder as is. Let’s look at an example:

Suzie is baking cookies and wants to divide them evenly among her 7 friends. She has 200 cookies. How many cookies will each friend get?

We can use long division to solve this: 200 / 7 = 28 with a remainder of 4. Each friend will get 28 cookies, but there will be 4 left over.

So should Suzie give 28 cookies to each friend and keep the remaining 4 for herself? It depends on the situation. If the cookies are going to be shared in a way that everyone gets an equal amount, it might be best to distribute the remaining 4 cookies so that everyone gets 29. But if Suzie is keeping the remaining cookies for herself, it might be okay to leave it as is.

Divisibility Rules

One way to make long division easier is to use divisibility rules. These are rules that help us quickly determine if a number is divisible by another number without having to go through the steps of long division.

• If a number ends in 0 or 5, it is divisible by 5.
• If a number ends in 0, it is divisible by any factor of 10.
• If a number ends in an even digit, it is divisible by 2.
• A number is divisible by 3 if the sum of its digits is divisible by 3.
• A number is divisible by 4 if its last two digits are divisible by 4.

There are many more divisibility rules, but these are some of the most commonly used.

Conclusion

Long division can be daunting at first, but with practice, it becomes easier. Remember to take your time, use divisibility rules when you can, and be patient. Math is a journey, and every step brings you closer to mastery.